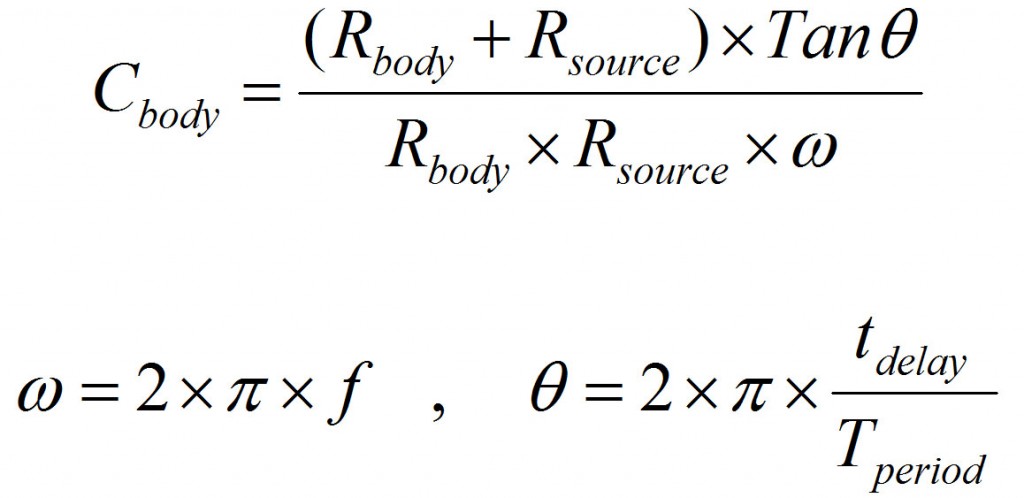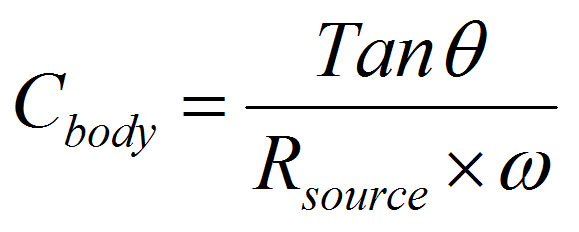AC hurts more than DC because of human body capacitance. But how big is this capacitance?
So there are multiple ways to measure capacitance, which I should say measuring current through a capacitor is not one of my favorites. Especially when it comes to measuring human body capacitance. But there are two more ways, both of which include placing a series resistor to the capacitor:
- Supply a square wave to the series resistor with other end of capacitor at ground. Measure the voltage across capacitor on a scope and see the exponential rise/fall of the voltage and calculate the capacitance.
- Supply a sinusoidal (sine) wave to the resistor and scope the output waveform and measure the delay between output and input and calculate capacitance.
I personally like the second method because the entire output wave shifts with the same delay. All you need to do is to compare the zero crossing of the input and output waves to find the delay. This can be easily made into a digital capacitance meter.
Capacitors resist against changes in voltage. When a series resistor is between the supply and a capacitor, capacitor causes a delay in output voltage and reduce its amplitude.
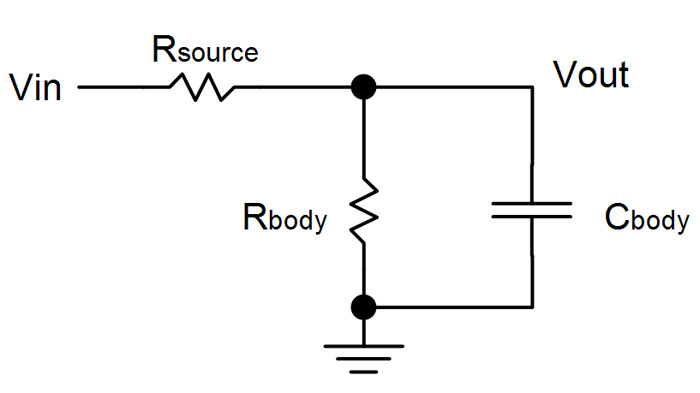
Human body have both a resistance and a capacitance in parallel. When a DC voltage is applied across body, only body resistance sends current through while for AC, it is both resistance and capacitance.
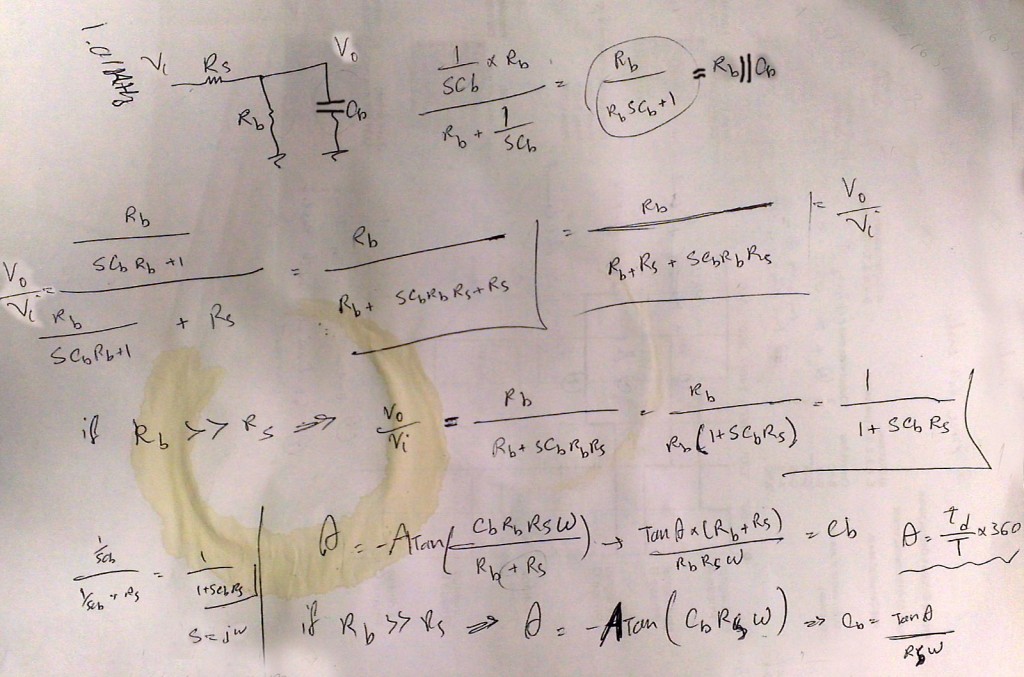
As shown in the following schematic, a series resistor is placed between supple (Vin) and body, which is called Rsource.
Now as you saw in the video, probing both Vin and Vout, you can measure the delay and calculate the capacitance using the following formula.
Cbody and Rbody are human body capacitance and resistance. You can measure the resistance using a multimeter. I measured my resistance over dry skin to be close to 1M Ohm. Different skin conditions changes this resistance.
Rsource is the series resistance you put between supply and body. You should choose this resistance properly to obtain proper accuracy. I used 100kOhm for frequencies of 100Hz and below, and 10kOhm for frequencies above 100Hz to 10kHz. To achieve more accurate results, it is good to keep the delay around 10% of the waveform period.
f in the above formula is the supply frequency, Tperiod = 1/f and tdelay is the measured delay between input and output waveforms.
For my measurements since my body resistance was close to 1M Ohm, I assumed Rbody >> Rsource, in which case you can simplify the formula as below:
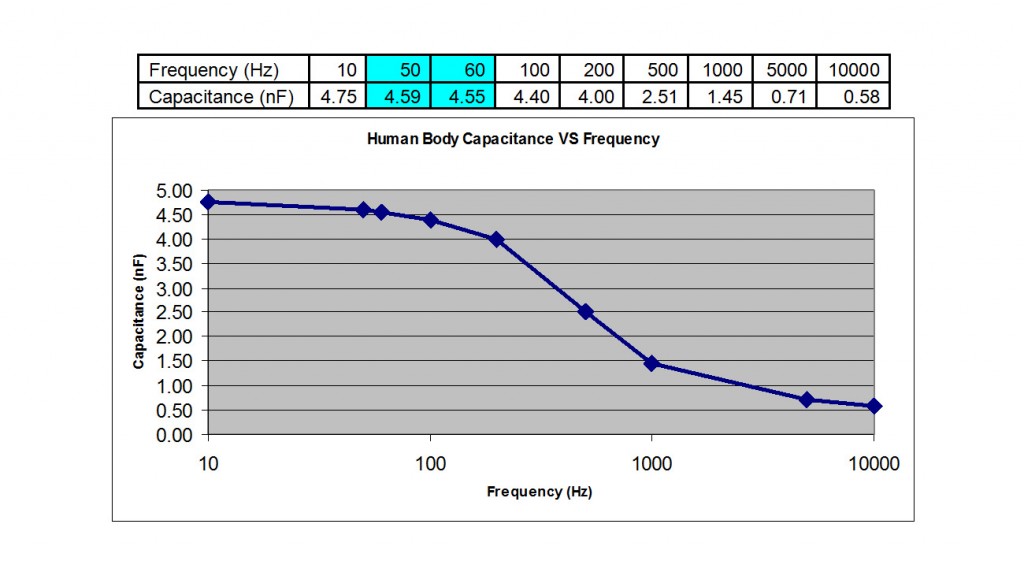
And so using this method, I measured my body capacitance at different frequencies which followed the following results:
The capacitance at 60Hz North American power line frequency is not huge. But the capacitor impedance is around 580 kOhm which in parallel to the 1M Ohm body resistance, it will result in around 500 kOhm total impedance. (you need to know how to calculate parallel/series impedance for this one).
So this means, for DC voltage you have 1M Ohm impedance (made of just resistance) while for 60Hz AC, you have 500 kOhm. So for some AC RMS value, the current through body is double compared to the same level DC voltage. and THAT’s why AC hurts way more than DC at the same level.
If you like to know how I come up with the formulas I showed above, following image shows my calculations.