Lichtenberg figures in wood are made through a fun, lethal process!
Lichtenberg figure is a general term for such figures made by high power electricity passing through wood, grass, glass or whatever, where the electricity can leave an impression. They look like a tree and its branches grown in hell!
 To make the figures on a wood:
To make the figures on a wood:
- Don’t use plywood like I did! a solid piece of wood does better.
- Mix two tea spoons of baking soda and water and wet the surface of the wood liberally. Let it sit a bit so the liquid can penetrate a bit. This makes the wood conductive and electricity can pass through it.
- Place electrodes on each side of the wood.
- Create high voltage across the electrodes, preferably over 2000V. Remember the source has to be able to supply large amounts of power to be able to burn the wood.
- NEVER EVER GET TOO CLOSE TO THE WOOD OR YOUR SUPPLY WHILE IT IS ON OR YOU DIE!
- As the wood heats up and burns your liquid dries up. It is better to wet it at the beginning and not in the middle of process though, otherwise it won’t look as good.
- If the electrodes are too close or there is too much liquid, they could arc like you saw in the video and leave giant burn marks!
Now to make high voltage, the easiest way is to use a transformer you can scavenge from old or broken microwave ovens. Quite dangerous and exposed, so be very careful. If you don’t know your way around electronic, just don’t do it!
Transformers are in general used to change the voltage and current levels between the input and output. In an ideal transformer, the “Active” input and output power are equal. The active power is what does the actual work such as generating heat. Of course there are other factors in real life that waste power such as winding wire resistances, transformer core losses and such. So the output power drops a bit as the efficiency is not 100%. But at least at no load we have the following equation:
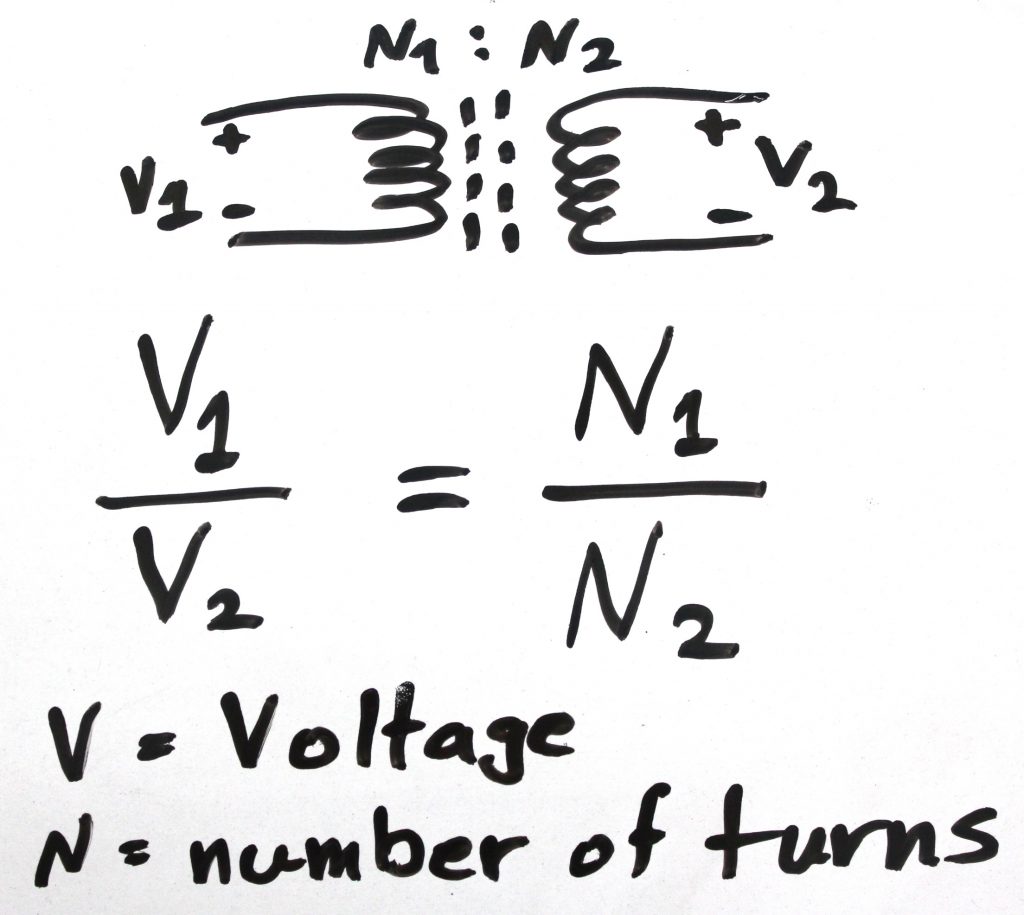 where N is the number of turns and V is the voltage. Also there is another useful equation to calculate the number of turns ratio if you can measure the inductance. Since the windings are both on the same core, the following equation provides relation between number of turns (Nx) and the inductance of primary and secondary (Lx):
where N is the number of turns and V is the voltage. Also there is another useful equation to calculate the number of turns ratio if you can measure the inductance. Since the windings are both on the same core, the following equation provides relation between number of turns (Nx) and the inductance of primary and secondary (Lx):
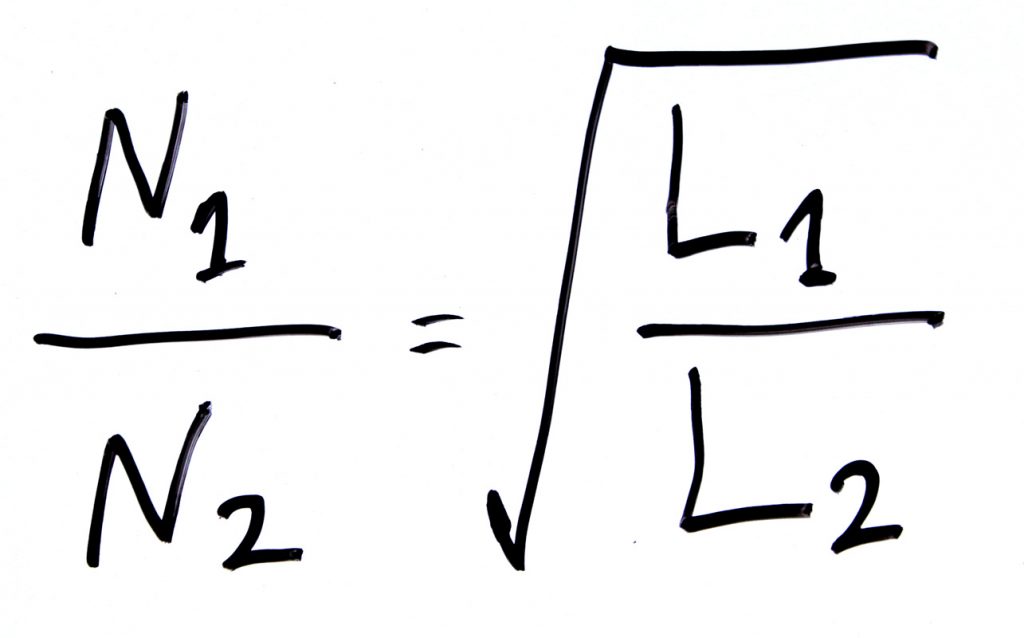 As mentioned in the video, any inductor results in a current lag, resulting in 90 degrees phase shift in an ideal inductor as shown in the picture below. At any moment of time power is equal to voltage times current. But as you see in the following picture, in some areas the power would be positive and in others negative depending on the voltage and current direction.
As mentioned in the video, any inductor results in a current lag, resulting in 90 degrees phase shift in an ideal inductor as shown in the picture below. At any moment of time power is equal to voltage times current. But as you see in the following picture, in some areas the power would be positive and in others negative depending on the voltage and current direction.
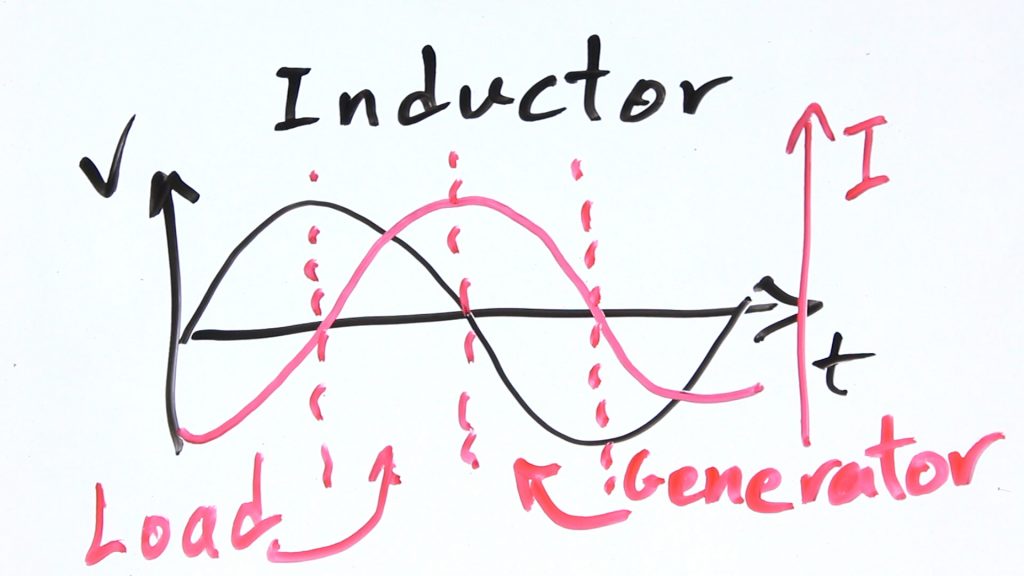 This means although when power is positive, the inductor pulls power from the supply, it puts the same amount of power back into the AC supply when the power is negative. So the net “Active” power consumption is zero. They call this “Reactive” power. It doesn’t do the work like generating heat.
This means although when power is positive, the inductor pulls power from the supply, it puts the same amount of power back into the AC supply when the power is negative. So the net “Active” power consumption is zero. They call this “Reactive” power. It doesn’t do the work like generating heat.
So in every transformer there is always some amount of current running into the primary (depending on the impedance of primary and loading) even if there is no load connected to the adapter. If there is any power drawn from the transformer, the phase shift is not 90 degrees any more and becomes less. So there is more power drawn from the source than the power returned to supply.
Now all inductor windings and power line wires have some small resistance and the transformers have their core losses. This means that this amount of current would generate some heat over resistive elements and such. This is one of the reasons old style transformers are not efficient, because even if you don’t use them to power anything but keep them plugged in, they still get warm and waste power. So the sooner you switch to switch-mode wall adapters,the better!
